Consideramos como (ángulo de inclinación) a aquel ángulo que se pueda presentar entre un segmento plano (Horizonte) y otro segmento distante.
Por ejemplo:

Dicha noción representa una pieza crucial, para algunas condiciones que se puedan presentar en un fenómenos naturales o producidos. Tal es el caso de la construcción de un puente que disponga de múltiples vías. Es necesario conocer la pendiente de una vía con respecto a otra para evitar una mala construcción del mismo.
Esta misma analogía podría ser ubicada en la comodidad del hogar, en las esquinas de las habitaciones. Si suponemos querer tener una habitación en la que la edificación de los cuartos cuadre es necesario, de cierta manera conocer a que ángulos inclinación estan dictadas las paredes.
Pues podría generarse una situación de una mala edificiación lo cual repercutiría en unos cuartos mal construidos. Todo estos detalles muy importantes para poder llevar un trabajo adelante.
Es por ello, que dicha noción debe ser tomada con seriedad pues uno nunca se imagina en la situación que podría ser útil.
La determinación del (ángulo de inclinación) ya en términos de su valor, es realizado bajo el contexto de la trigonometría por medio de la (Tangente y su función inversa) o bien a través del analísis vectorial.. Ambos caminos conduciendonos al mismo resultado.
En esta ocasión nos limitaremos al (Caso de la trigonometría), pues el otro caso sugiere concepciones de otros objetos aún no presentados o conocidos por muchas personas. Motivo por el cual se toma la consideración anterior.
Ahora bién, supongamos que tenemos un segmento (Horizonte) cuya longitud es de 2 metros y poseemos una altura de 4 metros del segmento (Horizonte) a el segmento distante y no conocemos la longitud del (Segmento distante).
Y por supuesto deseamos conocer el (valor del ángulo) comprendido entre estos 2 segmentos.. Entonces tendríamos una escenario similar a éste:

Para ello empleamos un poco de trigonometría utilizando la razón (Tangente) seguido de la ejecución de la función (Tangente inversa) para determinar el correspondiente ángulo, como se muestra en la imagen.
Suponiendo que podemos referenciar un marco, donde es posible establecer la distancia entre un segmento u otro.. Y que por extraña razón no conocemos el valor de un segmento, lo cual fuera ilógico deduciendo que pudimos establecer una altura..
Y por consiguiente debemos conocer la longitud del (segmento distante) ya que de no ser así no hubiera sido posible deducir un punto de donde fijar la altura que contemplamos.
Todo ello por supuesto considerando que el entorno, genera los elementos necesarios para la utilización de las razones trigonometrícas osea exista un triángulo rectángulo en él. Ya que de lo contrario sería necesario aplicar algunas leyes como: (Ley de los cosenos o ley de los senos) para conocer ello, ya que serían otra clase de triángulo.
Por el camino del (Analísis vectorial) se sugiere además de la noción de razones trigonometrícas, el conocimiento de la ubicación de los vectores dentro del marco de un (Sistema de coordenadas)..
En lo que ha (Pendiente de una recta) se refiere, consideramos como (Pendiente) aquella magnitud que expresa la variación o crecimiento de un objeto con respecto a sí mismo, por ejemplo: El caso de la recta, indica el crecimiento de la misma al cabo del paso de una unidad. Sirviendo dicho hecho como una base para la construcción de algunos otros objetos más complejos.
Como se muestra, en la imagen:

Esta noción es la asociación común de la razón trigonometríca (Tangente) a un ámbito de continuidad.
La determinación en el caso de la recta unicamente consiste en tomar dos coordenadas de la recta evaluarlas de acuerdo al cociente indicado en la imagen y listo!, Constatando que en una recta la pendiente siempre es constante por lo tanto no implica un reto de determinación, pero la pendiente de una curva no es del todo sencilla de determinar..
De ello se encarga el cálculo diferencial, como más adelante se observará.






 nos da la pendiente de la recta
nos da la pendiente de la recta  lo que nos lleva al caso anterior
lo que nos lleva al caso anterior es un vector direccional de la recta y tiene de componentes (x1-x0,y1-y0) y su pendiente será
es un vector direccional de la recta y tiene de componentes (x1-x0,y1-y0) y su pendiente será

 (constante).La ecuación de una recta vertical, tal como la v, responde a la ecuación general
(constante).La ecuación de una recta vertical, tal como la v, responde a la ecuación general  (constante).
(constante). .
.

 . Además, serán coincidentes cuando:
. Además, serán coincidentes cuando: 
 , es decir:
, es decir: 
 .
.

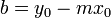


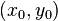 , el valor de m es la pendiente de cada una de las rectas que forman parte del haz, m puede tomar un valor real cualesquiera.
, el valor de m es la pendiente de cada una de las rectas que forman parte del haz, m puede tomar un valor real cualesquiera. como una
como una 
 es
es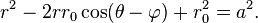
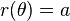

 donde
donde 


 (incluyendo al 0). Si k es un número entero, estas ecuaciones representan una rosa de k pétalos cuando k es
(incluyendo al 0). Si k es un número entero, estas ecuaciones representan una rosa de k pétalos cuando k es  para
para  , la gráfica de la ecuación:
, la gráfica de la ecuación:
 . Y si
. Y si 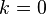 , la gráfica es una circunferencia de radio
, la gráfica es una circunferencia de radio 

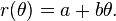

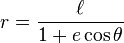
 es el semilado recto (la distancia perpendicular a un foco desde el eje mayor a la curva). Si e > 1, esta ecuación define una
es el semilado recto (la distancia perpendicular a un foco desde el eje mayor a la curva). Si e > 1, esta ecuación define una