 |
Tomando el valor positivo o negativo de la raíz según corresponda.
[.]Rectas notables
- La ecuación de una recta horizontal, tal como la h, responde a la ecuación general
 (constante).La ecuación de una recta vertical, tal como la v, responde a la ecuación general
(constante).La ecuación de una recta vertical, tal como la v, responde a la ecuación general  (constante).
(constante).
- Una recta trigonoidal, tal como la s, que pase por el origen O (0, 0), cumplirá la condición n = 0, siendo su ecuación:
 .
.
- Dos rectas cualesquiera:
- serán paralelas si y solo si
 . Además, serán coincidentes cuando:
. Además, serán coincidentes cuando: 
- serán perpendiculares si y sólo si
 , es decir:
, es decir: 
[.]Rectas que pasan por un punto
Determinar las rectas del plano que pasan por el punto  .
.
 .
.
La ecuación de la recta ha de ser, como ya se sabe:
Y ha de pasar por el punto  , luego tendrá que cumplirse:
, luego tendrá que cumplirse:
 , luego tendrá que cumplirse:
, luego tendrá que cumplirse:
Despejando b, tenemos esta ecuación:
Sustituyendo b en la ecuación general de la recta:
Ordenando términos:
Esta ecuación define un haz de rectas en el plano que pasa por el punto 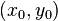 , el valor de m es la pendiente de cada una de las rectas que forman parte del haz, m puede tomar un valor real cualesquiera.
, el valor de m es la pendiente de cada una de las rectas que forman parte del haz, m puede tomar un valor real cualesquiera.
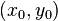 , el valor de m es la pendiente de cada una de las rectas que forman parte del haz, m puede tomar un valor real cualesquiera.
, el valor de m es la pendiente de cada una de las rectas que forman parte del haz, m puede tomar un valor real cualesquiera.



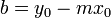


No hay comentarios:
Publicar un comentario